1020考研总结
Posted on Wed, 20 Oct 2010 13:16:29 -1100模电数电1020
§微变等效电路求解
§工作点稳定电路参量的计算
§差分放大电路
§数值转换,逻辑转换
- ●不管什么,先把等效电路画出来,直流+交流
-
●最大不失真输出电压
UCQ与UCC和UCES[有时按0→GND估算]之差的绝对值
如果问的是幅度则不需要除以√2,否则要除一下 -
●常见的稳定电路要引入负反馈
比如增加射极电阻,以及在基集间增加电阻 - ●通过射极电阻引入负反馈若不加旁路电容,可以使电压放大倍数与β无关(-RL'/RE),但放大倍数较有旁路电容时大大缩小
-
●抑制温度漂移的方法
- 引入直流负反馈
- 采用温度补偿的方法,利用热敏元件[比如热敏电阻和二极管<2.4.5>]抵消放大管的变化
- 采用特性相同的管子,构成"差分放大电路"
- ●单管共射频率参数,相位中频-180°,低频-90°,高频-270°
- 负数:原码→除符号位取反→反码→+1→补码
- 10进制小数化为二进制时用乘二取一并去一的方法[总结的不好,凑合着记忆了]
- 与或→与非--与非:X→(X')'
- 与或→与或非:Y+Y'=1,卡诺图0的反
- 与或→或非-或非:先化成与或非,再X→(X')'
下面测试下用ScribeFire插图,貌似没法更改投稿选项,这个不应投的啊....
http://mblogpic.store.qq.com/mblogpic/56a76b98890049f95506/2000
![\underset{[a,b]}{max}f^{\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime}(x)=M](/user_files/pingf/epics/a92840f9f2cc38dbf18b6d66735d624a421ea0bb.png) 且有f(a)=0证明
且有f(a)=0证明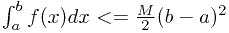
![\underset{[a,b]}{max}f^{\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime}(x)=M](/user_files/pingf/epics/cb94cc3e9a5e2d392070c05f3dc2b23b18419935.png) 且有f(a)=f(b)=0证明
且有f(a)=f(b)=0证明 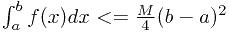
![\underset{[a,b]}{max}f^{\,\prime\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime\,\prime}(x)=M](/user_files/pingf/epics/b86ab626385bfdae1255928889f2005534eb44a6.png) 且有f(a)=f(b)=0证明
且有f(a)=f(b)=0证明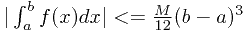
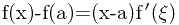
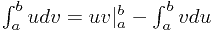 对于上面这类题目还要进行一些配凑,如
对于上面这类题目还要进行一些配凑,如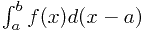 或者是
或者是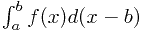
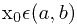 时的
时的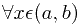 有
有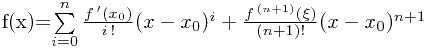 其中
其中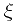 在x到
在x到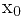 之间
之间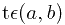 ,则f(t)可表示为
,则f(t)可表示为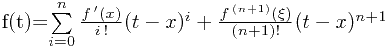 其中
其中