[好文备份]高树的故事
Posted on Thu, 26 Aug 2010 12:08:16 -1100很久很久以前,在拉格朗日照耀下,有几座城:分别是常微分方城和偏微分方城这两座兄弟城,还有数理方城、随机过城。从这几座城里流出了几条溪,比较 著名的有:柯溪、数学分溪、泛函分溪、回归分溪、时间序列分溪等。其中某几条溪和支流汇聚在一起,形成了解析几河、微分几河、黎曼几河三条大河。
河边有座古老的海森堡,里面生活着亥霍母子,穿着德布罗衣、卢瑟服、门捷列服,这样就不会被开尔蚊骚扰,被河里的薛定鳄咬伤。城堡 门口两边摆放着牛墩和道尔墩,出去便是鲍林。鲍林里面的树非常多:有高等代树、抽象代树、线性代树、实变函树、复变函树、数值代树等,还有长满了傅立叶, 开满了范德花的级树。。。。人们专门在这些树边放了许多的盖(概)桶,高桶,这是用来放尸体的,因为,挂在上面的人,太多了,太多了。。。。这些人死后就 葬在微积坟,坟的后面是一片广阔的麦克劳林,林子里有一只费马,它喜欢在柯溪喝水,溪里撒着用高丝做成的ε-网,有时可以捕捉到二次剩鱼。
后来,芬斯勒几河改道,几河不能同调,工程师李群不得不微分流形,调河分溪。几河分溪以后,水量大涨,建了个测渡也没有效果,还是挂了很多人,连非交换代树都挂满了,不得不弄到动力系桶里扔掉。
有些人不想挂在树上,索性投入了数值逼井(近)。结果投井的人发现井下生活着线性回龟和非线性回龟两种龟:前一种最为常见的是简单线性回龟和多元线性回龟,它们都喜欢吃最小二橙。
柯溪经过不等市,渐近县和极县,这里房子的屋顶都是用伽罗瓦盖的,人们的主食是无穷小粮。
极县旁有一座道观叫线性无观,线性无观里有很多道士叫做多项士,道长比较二,也叫二项士。线性无观旁有一座庙叫做香寺,长老叫做满 志,排出咀阵,守卫着一座塔方。一天二项士拎着马尔可夫链来踢馆,满志曰:“正定!正定!吾级数太低,愿以郑太求和,道友合同否?”二项士惊呼:“特真值 啊!”立退。不料满志此人置信度太低,不以郑太求和,却要郑太回归。二项式大怒在密度函树下展开标准分布,布里包了两个钗钗,分别是标准钗和方钗。满志见 状央(鞅)求饶命。二项式将其关到希尔伯特空间,命巴纳赫看守。后来,巴纳赫让其付饭钱,满志念已缴钱便贪多吃,结果在无参树下被噎死(贝叶 斯)。。。。。
![\underset{[a,b]}{max}f^{\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime}(x)=M](/user_files/pingf/epics/a92840f9f2cc38dbf18b6d66735d624a421ea0bb.png) 且有f(a)=0证明
且有f(a)=0证明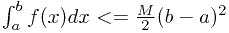
![\underset{[a,b]}{max}f^{\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime}(x)=M](/user_files/pingf/epics/cb94cc3e9a5e2d392070c05f3dc2b23b18419935.png) 且有f(a)=f(b)=0证明
且有f(a)=f(b)=0证明 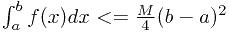
![\underset{[a,b]}{max}f^{\,\prime\,\prime}(x)=M \underset{[a,b]}{max}f^{\,\prime\,\prime}(x)=M](/user_files/pingf/epics/b86ab626385bfdae1255928889f2005534eb44a6.png) 且有f(a)=f(b)=0证明
且有f(a)=f(b)=0证明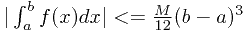
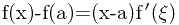
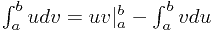 对于上面这类题目还要进行一些配凑,如
对于上面这类题目还要进行一些配凑,如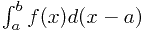 或者是
或者是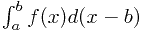
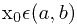 时的
时的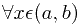 有
有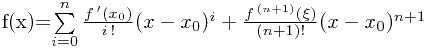 其中
其中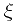 在x到
在x到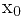 之间
之间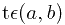 ,则f(t)可表示为
,则f(t)可表示为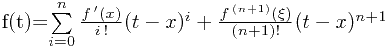 其中
其中